Stats Bootcamp - class 14

Hypothesis testing

Neelanjan Mukherjee

RNA Bioscience Initiative | CU Anschutz

2024-10-21

Prepare mouse biochem data

# we are reading the data directly from the internet
biochem <- read_tsv("http://mtweb.cs.ucl.ac.uk/HSMICE/PHENOTYPES/Biochemistry.txt", show_col_types = FALSE) |>
  janitor::clean_names()

# simplify names a bit more
colnames(biochem) <- gsub(pattern = "biochem_", replacement = "", colnames(biochem))

# we are going to simplify this a bit and only keep some columns
keep <- colnames(biochem)[c(1, 6, 9, 14, 15, 24:28)]
biochem <- biochem[, keep]

# get weights for each individual mouse
# careful: did not come with column names
weight <- read_tsv("http://mtweb.cs.ucl.ac.uk/HSMICE/PHENOTYPES/weight", col_names = F, show_col_types = FALSE)

# add column names
colnames(weight) <- c("subject_name", "weight")

# add weight to biochem table and get rid of NAs
# rename sex to sex
b <- inner_join(biochem, weight, by = "subject_name") |>
  na.omit() |>
  rename(sex = gender)

Learning objectives

  • Formulate and Execute null hypothesis testing
  • Identify and Perform the proper statistical test for data type/comparison
  • Calculate and Interpret p-values

Random variables

Response Variable ( y - aka dependent or outcome variable): this variable is predicted or its variation is explained by the explanatory variable. In an experiment, this is the outcome that is measured following manipulation of the explanatory variable.

Explanatory Variable ( x - aka independent or predictor variable): explains variations in the response variable. In an experiment, it is manipulated by the researcher.

The simplicity underlying common tests

Most of the common statistical models (t-test, correlation, ANOVA; etc.) are special cases of linear models or a very close approximation. This simplicity means that there is less to learn. It all comes down to:

\(y = a \cdot x + b\)

This needless complexity multiplies when students try to rote learn the parametric assumptions underlying each test separately rather than deducing them from the linear model.

Stats equation for a line

Model:

\(y\) equals the intercept (\(\beta_0\)) pluss a slope (\(\beta_1\)) times \(x\).

\(y = \beta_0 + \beta_1 x \qquad \qquad \mathcal{H}_0: \beta_1 = 0\)

… which is the same as \(y = b + a \cdot x\).

The short hand for this in R: y ~ 1 + x

R interprets this as:

y = 1*number + x*othernumber

The task of t-tests, lm, etc., is simply to find the numbers that best predict \(y\).

Appropriate statistical test cheatsheet

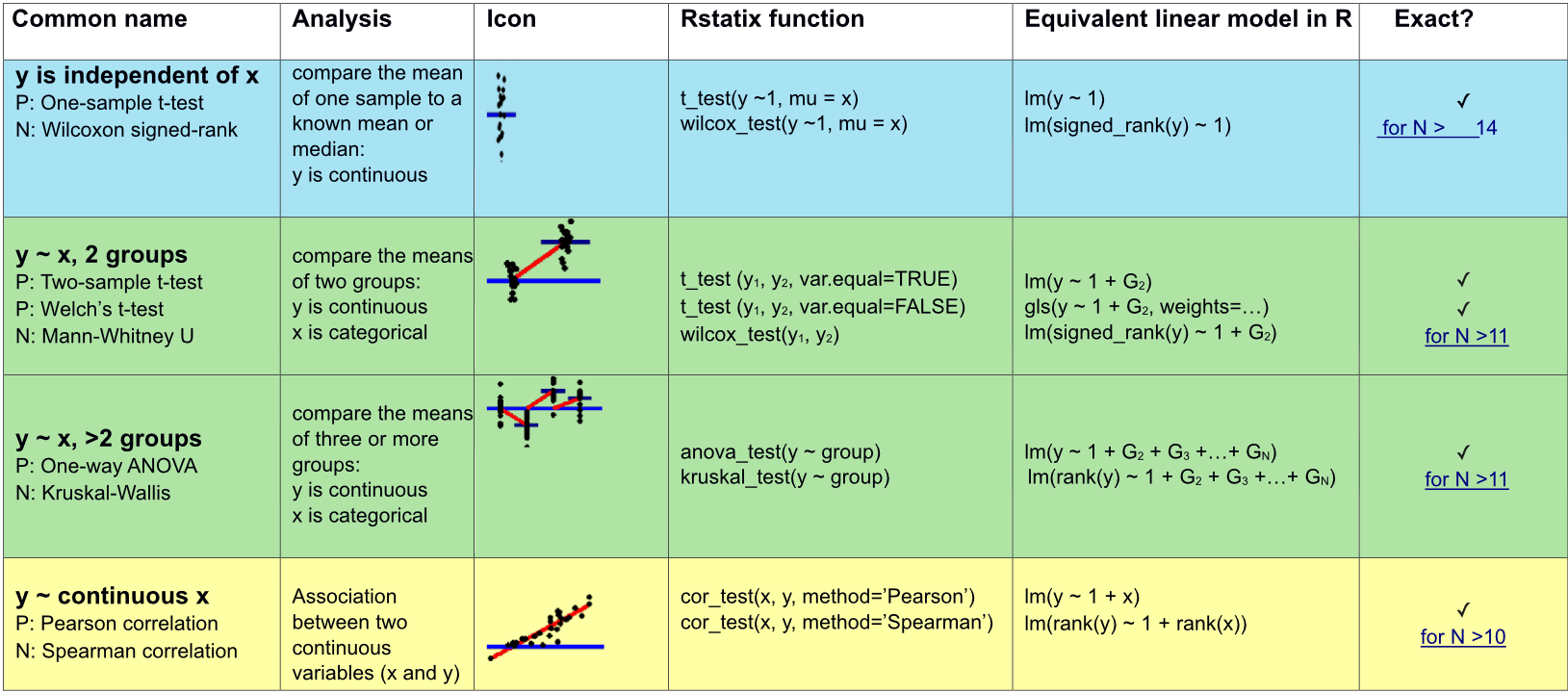
Comparing means between two groups

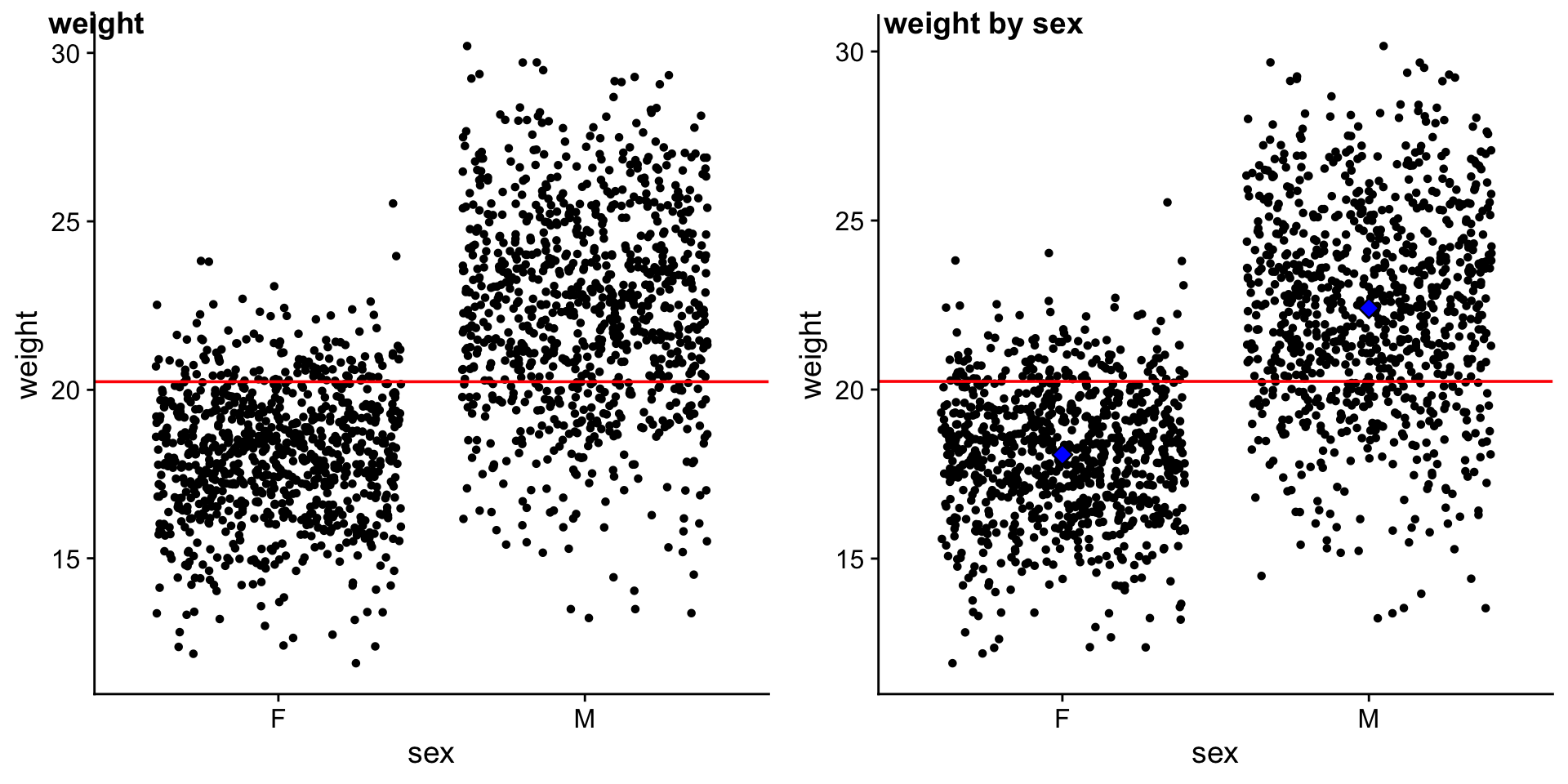
We will compare mouse \(weight\) by \(sex\).

# plot weight by sex
p_ws <- ggplot(
  b,
  aes(x = sex, y = weight)
) +
  geom_jitter(size = 1) +
  geom_hline(
    yintercept = mean(b$weight),
    color = "red"
  ) +
  theme_cowplot()


# plot weight by sex with mean weight and mean weight by sex
p_ws2 <- ggplot(
  b,
  aes(x = sex, y = weight)
) +
  geom_jitter(size = 1) +
  geom_hline(
    yintercept = mean(b$weight),
    color = "red"
  ) +
  stat_summary(fun = "mean", geom = "point", fill = "blue", shape = 23, size = 3) +
  theme_cowplot()

plot_grid(p_ws, p_ws2, ncol = 2, labels = c("weight", "weight by sex"), scale = c(1, 1))

Comparing means between two groups

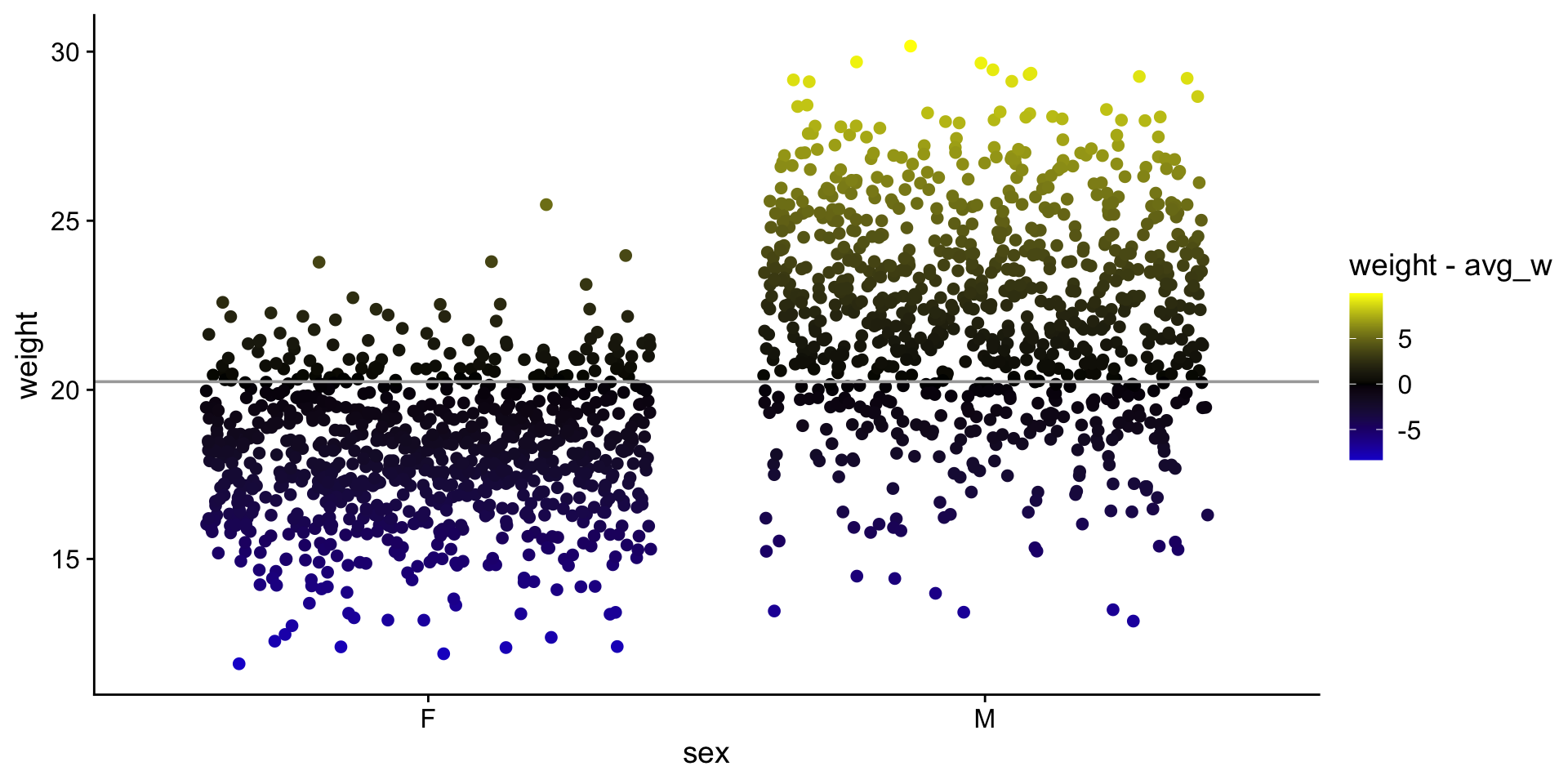
STEP 1: Can mouse sex explain mouse weight?

Model: \(y_{i} = \beta_0 \cdot 1+ \beta_1 \cdot x_{i}\)

Null Hypothesis: \(\mathcal{H}_0: \beta_1 = 0\)

\(\mathcal{H}_0:\) mouse \(sex\) does NOT explain \(weight\)

Alternative Hypothesis: \(\mathcal{H}_1: \beta_1 \neq 0\)

\(\mathcal{H}_1:\) mouse \(sex\) does explain \(weight\)

Important: \(x_{i}\) is an indicator (0 or 1) saying whether data point i was sampled from one or the other group (female or male).

We will explore this in more detail soon.

STEP 2: Fit linear model and examine results

fit_ws <- lm(formula = weight ~ 1 + sex, data = b)

Fit summary:

glance(fit_ws) |>
  gt() |>
  fmt_number(columns = r.squared:statistic, decimals = 3)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.421 0.421 2.538 1,296.507 9.251047e-214 1 -4187.427 8380.854 8397.31 11467.91 1780 1782

Coefficient summary:

tidy(fit_ws) |>
  gt() |>
  fmt_number(columns = estimate:statistic, decimals = 3)
term estimate std.error statistic p.value
(Intercept) 18.076 0.085 212.572 0.000000e+00
sexM 4.330 0.120 36.007 9.251047e-214

Collecting residuals and other information

add residuals and other information

# augment
b_ws <- augment(fit_ws, data = b)

# mean weight
avg_w <- mean(b_ws$weight)

w <- b |>
  group_by(sex) |>
  get_summary_stats(weight, type = "mean")
# mean weight female
avg_wf <- pull(w[1, 4])
avg_wf
[1] 18.076
# mean weight male
avg_wm <- pull(w[2, 4])
avg_wm
[1] 22.406

STEP 3: Visualize the error around fit

# plot of data with mean and colored by residuals
p_ws <- ggplot(
  b_ws,
  aes(x = sex, y = weight)
) +
  geom_point(
    position = position_jitter(),
    aes(color = .resid)
  ) +
  scale_color_gradient2(
    low = "blue",
    mid = "black",
    high = "yellow"
  ) +
  geom_hline(
    yintercept = avg_w,
    color = "darkgrey"
  ) +
  geom_segment(
    aes(
      x = .5, xend = 1.5,
      y = avg_wf, yend = avg_wf
    ),
    color = "red"
  ) +
  geom_segment(
    aes(
      x = 1.5, xend = 2.5,
      y = avg_wm
    ),
    yend = avg_wm,
    color = "red"
  ) +
  theme_cowplot()

p_ws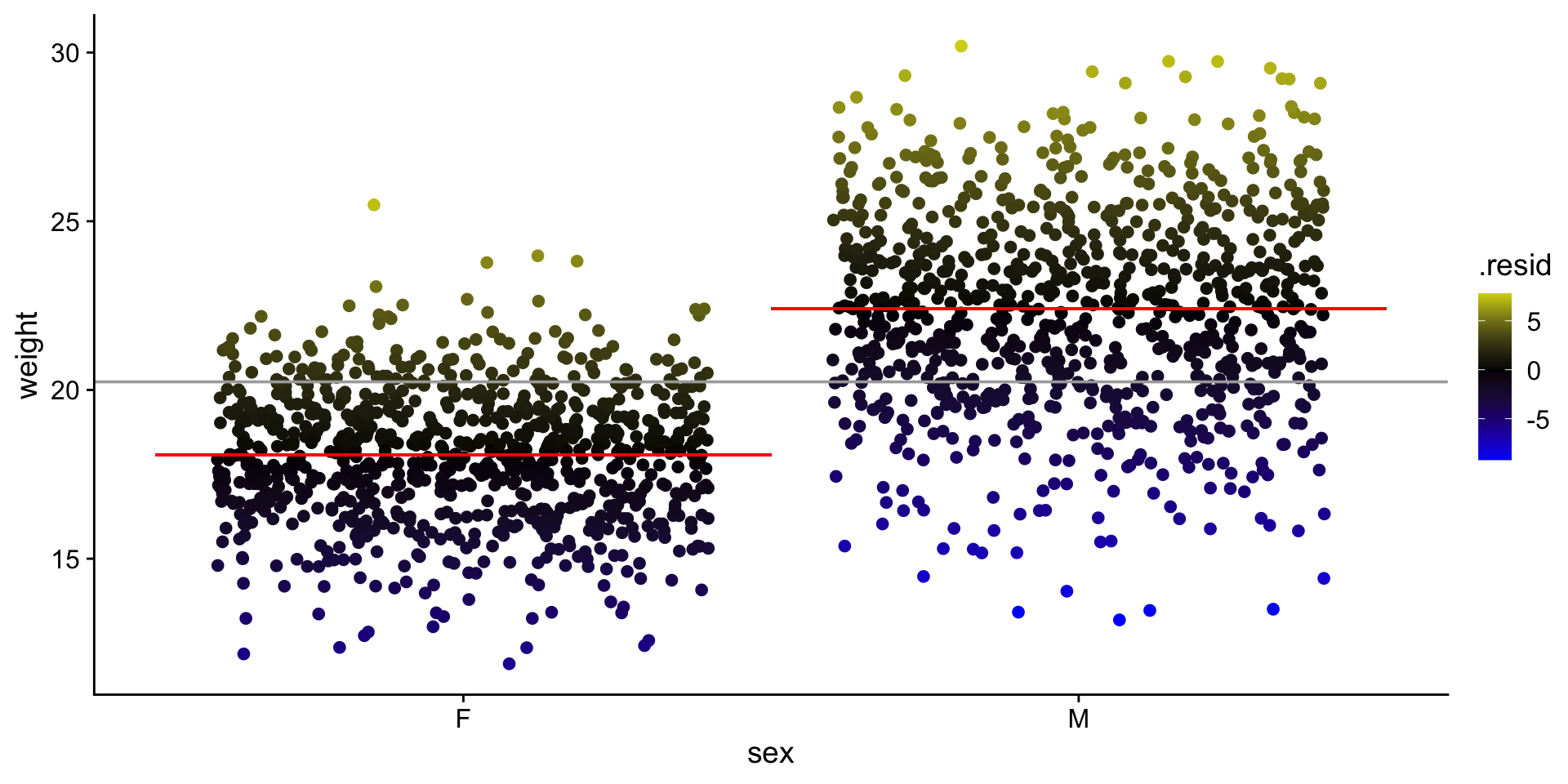

STEP 4: Visualize the error around the null (mean weight)

p_w <- ggplot(
  b_ws,
  aes(x = sex, y = weight)
) +
  geom_point(
    position = position_jitter(),
    aes(color = weight - avg_w)
  ) +
  scale_color_gradient2(
    low = "blue",
    mid = "black",
    high = "yellow"
  ) +
  geom_hline(
    yintercept = avg_w,
    color = "darkgrey"
  ) +
  theme_cowplot()

p_w

Compare fit error to null error graphically

plot_grid(p_ws, p_w, ncol = 2, labels = c("weight by sex", "weight by intercept"))

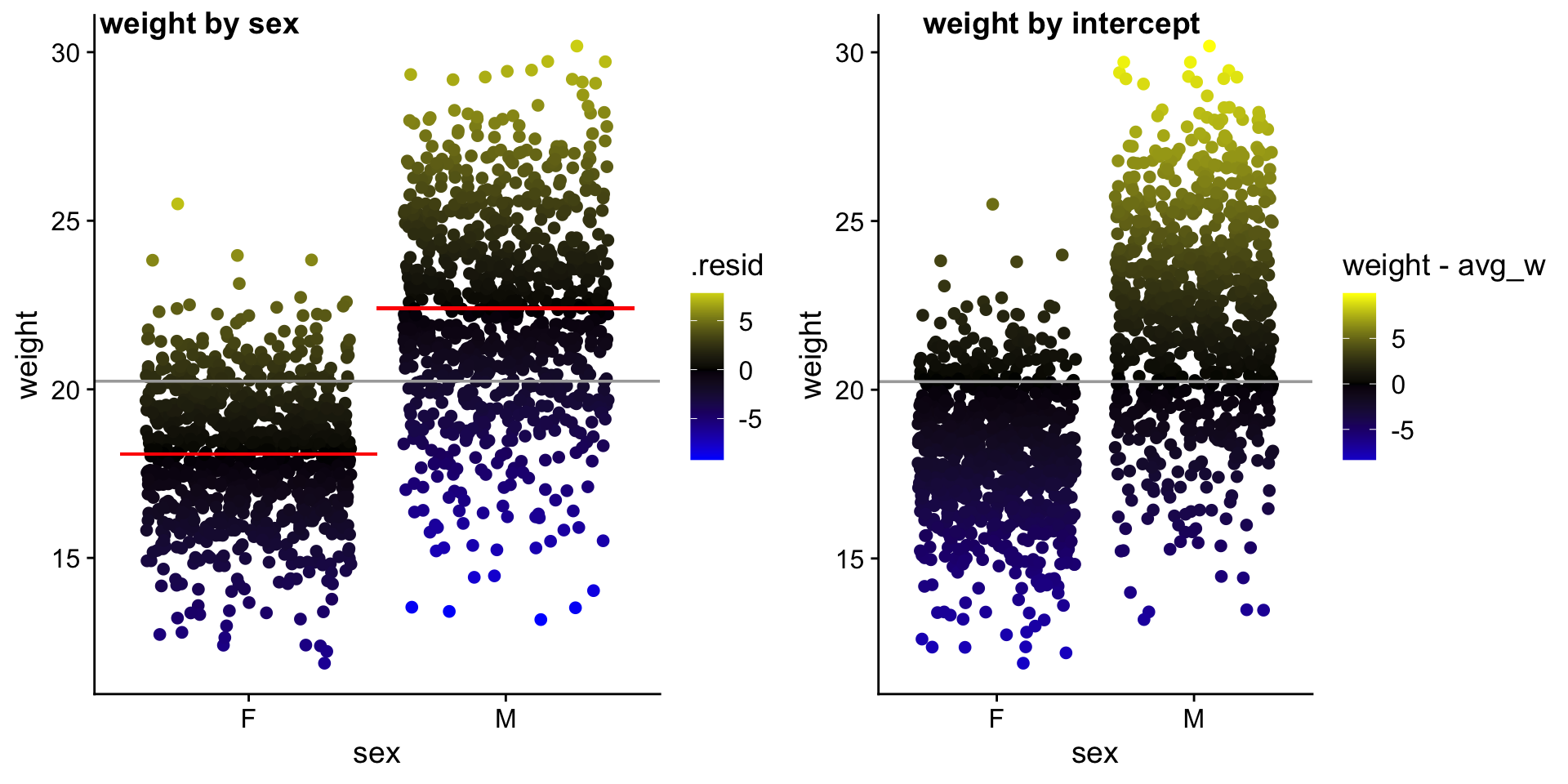
We are fitting 2 lines to the data. For the weight by sex model of the fit (left), we fit 2 lines. For the weight by null model (right) we fit 1 line.

Exceptions: mice with highest residuals

subject_name weight sex .resid .fitted
A084124895 30.20 M 7.79 22.41
A067109771 25.50 F 7.42 18.08
A084126258 29.70 M 7.29 22.41
A084286127 29.70 M 7.29 22.41
A064096308 29.50 M 7.09 22.41
A084127035 29.40 M 6.99 22.41
A063571569 29.30 M 6.89 22.41
A067018569 29.30 M 6.89 22.41
A084284841 29.20 M 6.79 22.41
A084285310 29.20 M 6.79 22.41
A084287792 29.10 M 6.69 22.41
A084291785 29.10 M 6.69 22.41
A064063035 28.70 M 6.29 22.41
A063820626 28.40 M 5.99 22.41
A084286862 28.40 M 5.99 22.41

Matrices Interlude Begin

How do we go from 2 fit lines to 1 equation

Since we don’t want to calculate any of this by hand, the framework needs to be flexible such that a computer can execute for different flavors of comparison (cont y vs cont x, cont y vs 2 or more categorical x, …).

Let’s focus on just a few mice

Remember that:
\(weight\) is \(y\)
\(F_{avg}\) is the average \(weight\) of \(females\)
\(M_{avg}\) is the average \(weight\) of \(males\)

A048054885, female
\(y_{85}= 1 \cdot F_{avg} + 0 \cdot M_{avg} + residual_{85}\)

A067109771, female
\(y_{71}= 1 \cdot F_{avg} + 0 \cdot M_{avg} + residual_{71}\)

A066822351, male
\(y_{51}= 0 \cdot F_{avg} + 1 \cdot M_{avg} + residual_{51}\)

A048274362, male
\(y_{62}= 0 \cdot F_{avg} + 1 \cdot M_{avg} + residual_{62}\)

Let’s focus on just a few mice

subject_name weight sex .fitted .resid
A048054885 24.0 F 18.07587 5.924130
A067109771 25.5 F 18.07587 7.424130
A048274362 13.4 M 22.40595 -9.005948
A066822351 13.2 M 22.40595 -9.205948

Need a volunteer

Me: Ooohh my, imagine how tedious it would be to do this for all 1782 mice…
Volunteer: Wait a sec…isn’t there a way to formulate this as a matrix algebra problem.
Me: You’re right - I’m so glad you asked! Let’s conjur matrix-magic to solve this problem..

\(f_{avg} = \beta_0\) is the average \(weight\) of \(female\) mice
\(m_{avg} = \beta_1\) is the average \(weight\) of \(male\) mice

\(\begin{bmatrix} y_{85} \\ y_{71} \\ y_{51} \\y_{62} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} + \begin{bmatrix} e_{85} \\ e_{71} \\ e_{51} \\e_{62} \end{bmatrix}\)

So basically this looks like the same equation for fitting a line we’ve been discussing, just w/a few more dimensions :)

This is a conceptual peak into the underbelly of how the \(\beta\) cofficients and least squares is performed using matrix operations (linear algebra). If you are interested in learning more see references at the end of the slides.

Matrices Interlude FIN

Calculate \(R^2\)

\(SS_{fit}\) — sum of squared errors around the least-squares fit

ss_fit <- sum(b_ws$.resid^2)
ss_fit
[1] 11467.91

\(SS_{null}\) — sum of squared errors around the mean of \(y\)

ss_null <- sum(
  (b_ws$weight - avg_w)^2
)
ss_null
[1] 19820.85

\(R^2 = 1 - \displaystyle \frac {SS_{fit}}{SS_{null}}\)

rsq <- 1 - ss_fit / ss_null
rsq
[1] 0.4214218
glance(fit_ws) |> select(r.squared)
# A tibble: 1 x 1
  r.squared
      <dbl>
1     0.421

Woohoo!!

Compare to traditional t-test

b |>
  t_test(weight ~ 1 + sex) |>
  select(-c(n1, n2, df)) |>
  gt()
.y. group1 group2 statistic p
weight F M -36.00705 1.86e-206 
tidy(fit_ws) |>
  select(term, estimate, statistic, p.value) |>
  gt()
term estimate statistic p.value
(Intercept) 18.075870 212.57194 0.000000e+00
sexM 4.330079 36.00705 9.251047e-214

prep data for fams

# i have pre-selected some families to compare
myfams <- c(
  "B1.5:E1.4(4) B1.5:A1.4(5)",
  "F1.3:A1.2(3) F1.3:E2.2(3)",
  "A1.3:D1.2(3) A1.3:H1.2(3)",
  "D5.4:G2.3(4) D5.4:C4.3(4)"
)

# only keep the familys in myfams
bfam <- b |>
  filter(family %in% myfams) |>
  droplevels()

# simplify family names and make factor
bfam$family <- gsub(pattern = "\\..*", replacement = "", x = bfam$family) |>
  as.factor()


# make B1 the reference (most similar to overall mean)
bfam$family <- relevel(x = bfam$family, ref = "B1")

STEP 1: Can family explain weight?

ANOVA -> comparing means of 3 or more groups.

Let’s compare the \(weight\) by \(family\), but only for a few selected families.

ggplot(
  data = bfam,
  aes(y = weight, x = family, color = family)
) +
  geom_jitter(width = .2) +
  theme_cowplot()

STEP 1: Can family explain weight?

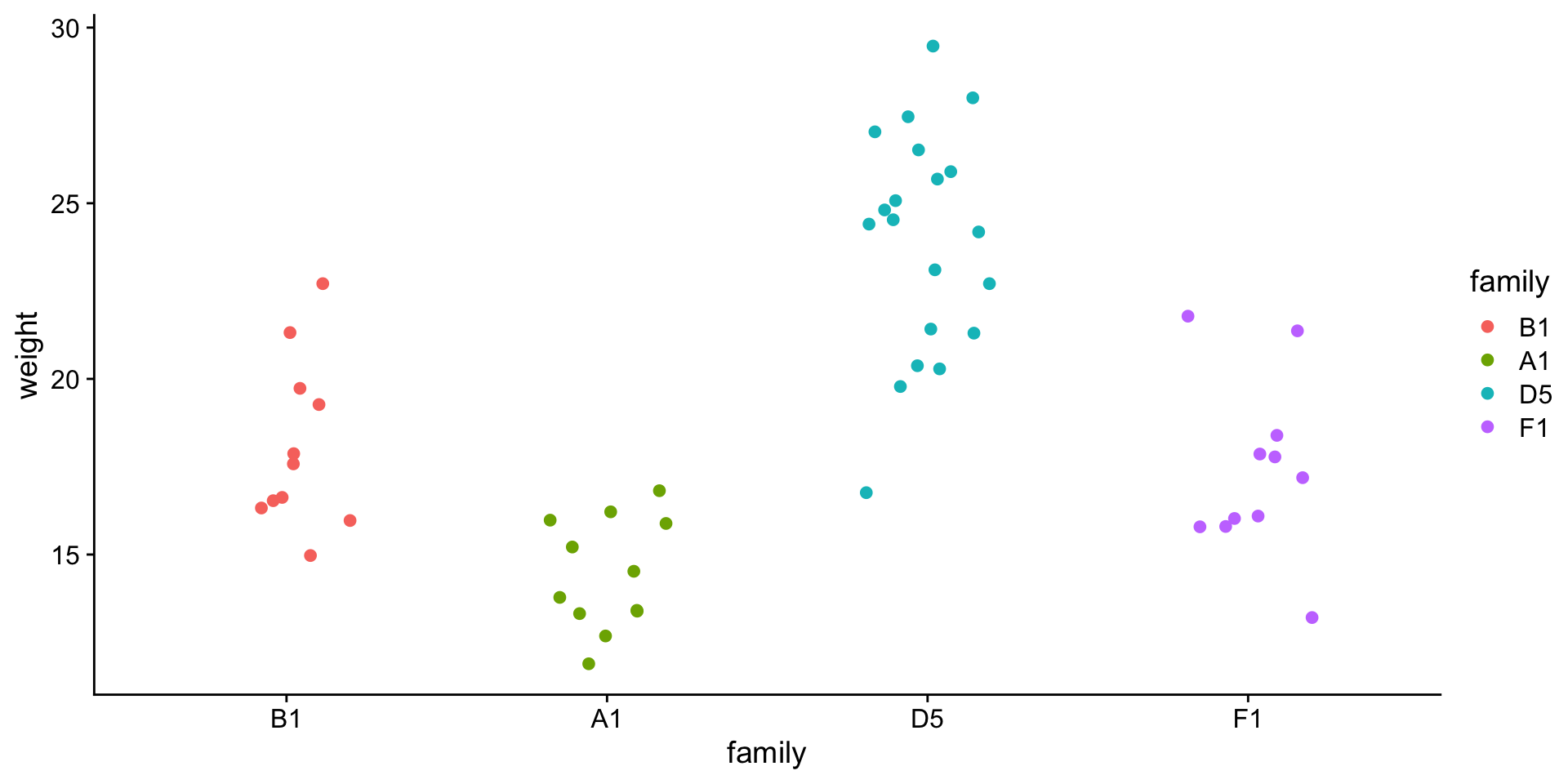
What does the model look like?

Model: \(y_{i} = \beta_0 \cdot 1+ \beta_1 \cdot x_{i}\)

Null Hypothesis: \(\mathcal{H}_0: \beta_1 = 0\)

\(\mathcal{H}_0:\) mouse \(family\) does NOT explain \(weight\)

Alternative Hypothesis: \(\mathcal{H}_1: \beta_1 \neq 0\)

\(\mathcal{H}_1:\) mouse \(family\) does explain \(weight\)

Important: \(x_{i}\) is an indicator (0 or 1) saying which group point \(i\) was sampled from using the matrix encoding of 0s and 1s.

Below is an example depicting 6 observations with 2 from each of 3 families:

\(\begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \\y_{4} \\y_{5} \\y_{5} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} + \begin{bmatrix} e_{1} \\ e_{2} \\ e_{3} \\e_{4} \\e_{5} \\e_{6} \end{bmatrix}\)

STEP 2: Fit linear model and examine results

fit_wf <- lm(formula = weight ~ 1 + family, data = bfam)

Fit summary:

glance(fit_wf) |>
  gt() |>
  fmt_number(columns = r.squared:statistic, decimals = 3)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.692 0.674 2.620 37.514 7.615782e-13 3 -126.5631 263.1262 273.0711 343.3084 50 54

Coefficient summary:

tidy(fit_wf) |>
  gt() |>
  fmt_number(columns = estimate:statistic, decimals = 3)
term estimate std.error statistic p.value
(Intercept) 18.082 0.790 22.887 3.754848e-28
familyA1 −3.657 1.094 −3.343 1.574764e-03
familyD5 5.863 0.984 5.961 2.518066e-07
familyF1 −0.682 1.117 −0.610 5.444740e-01

Collecting residuals and other information

add residuals and other information

# augment
b_wf <- augment(fit_wf, data = bfam)

# mean weight per fam
mean_B1 <- fit_wf$coefficients[1]

mean_A1 <- fit_wf$coefficients[1] +
  fit_wf$coefficients[2]

mean_D5 <- fit_wf$coefficients[1] +
  fit_wf$coefficients[3]

mean_F1 <- fit_wf$coefficients[1] +
  fit_wf$coefficients[4]

STEP 3: Visualize the error around fit

ggplot(
  b_wf,
  aes(x = family, y = weight)
) +
  geom_point(
    position = position_jitter(),
    aes(color = .resid)
  ) +
  scale_color_gradient2(
    low = "blue",
    mid = "black",
    high = "yellow"
  ) +
  geom_segment(aes(x = .5, xend = 1.5, y = mean_B1, yend = mean_B1), color = "red") +
  geom_segment(aes(x = 1.5, xend = 2.5, y = mean_A1, yend = mean_A1), color = "red") +
  geom_segment(aes(x = 2.5, xend = 3.5, y = mean_D5, yend = mean_D5), color = "red") +
  geom_segment(aes(x = 3.5, xend = 4.5, y = mean_F1, yend = mean_F1), color = "red") +
  geom_segment(aes(x = .5, xend = 4.5, y = mean(weight), yend = mean(weight)), color = "black") +
  theme_cowplot()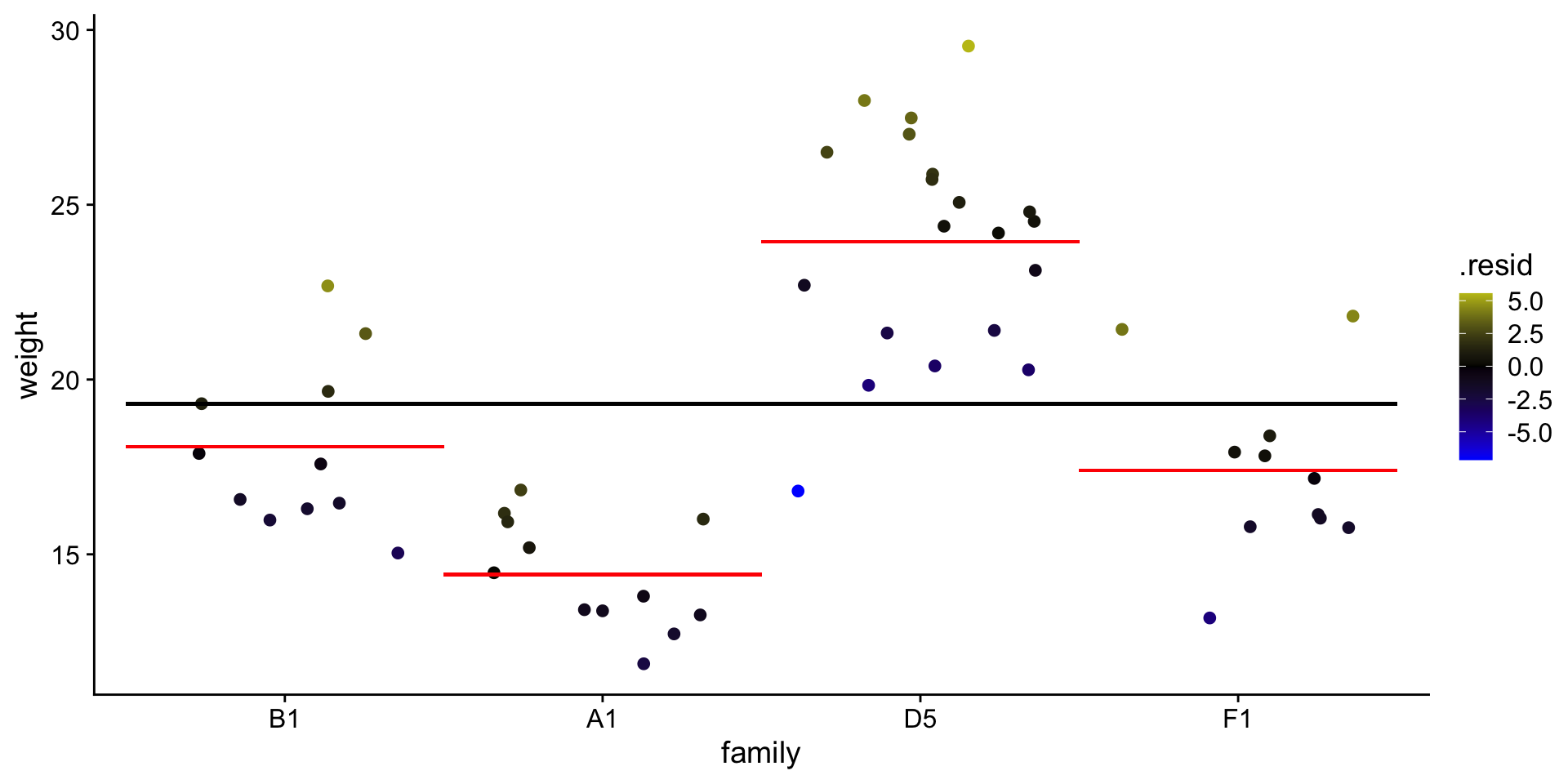

STEP 3: Visualize the error around fit

Compare to traditional ANOVA

bfam |>
  anova_test(weight ~ 1 + family) |>
  gt()
Effect DFn DFd F p p<.05 ges
family 3 50 37.514 7.62e-13 * 0.692 
tidy(fit_wf) |>
  select(term, estimate, statistic, p.value) |>
  gt()
term estimate statistic p.value
(Intercept) 18.0818182 22.8865985 3.754848e-28
familyA1 -3.6568182 -3.3432529 1.574764e-03
familyD5 5.8631818 5.9608290 2.518066e-07
familyF1 -0.6818182 -0.6102288 5.444740e-01

Comparing 2 groups of 2 continuous variables

ANCOVA, Analysis of Covariance. ANOVA with more than one independent variable. What is the impact of mouse age on mouse weight for males vs females.

ggplot(data = b, aes(y = weight, x = age, color = sex)) +
  geom_point(size = .5) +
  geom_smooth(method = lm) +
  theme_cowplot()

Comparing 2 groups of 2 continuous variables

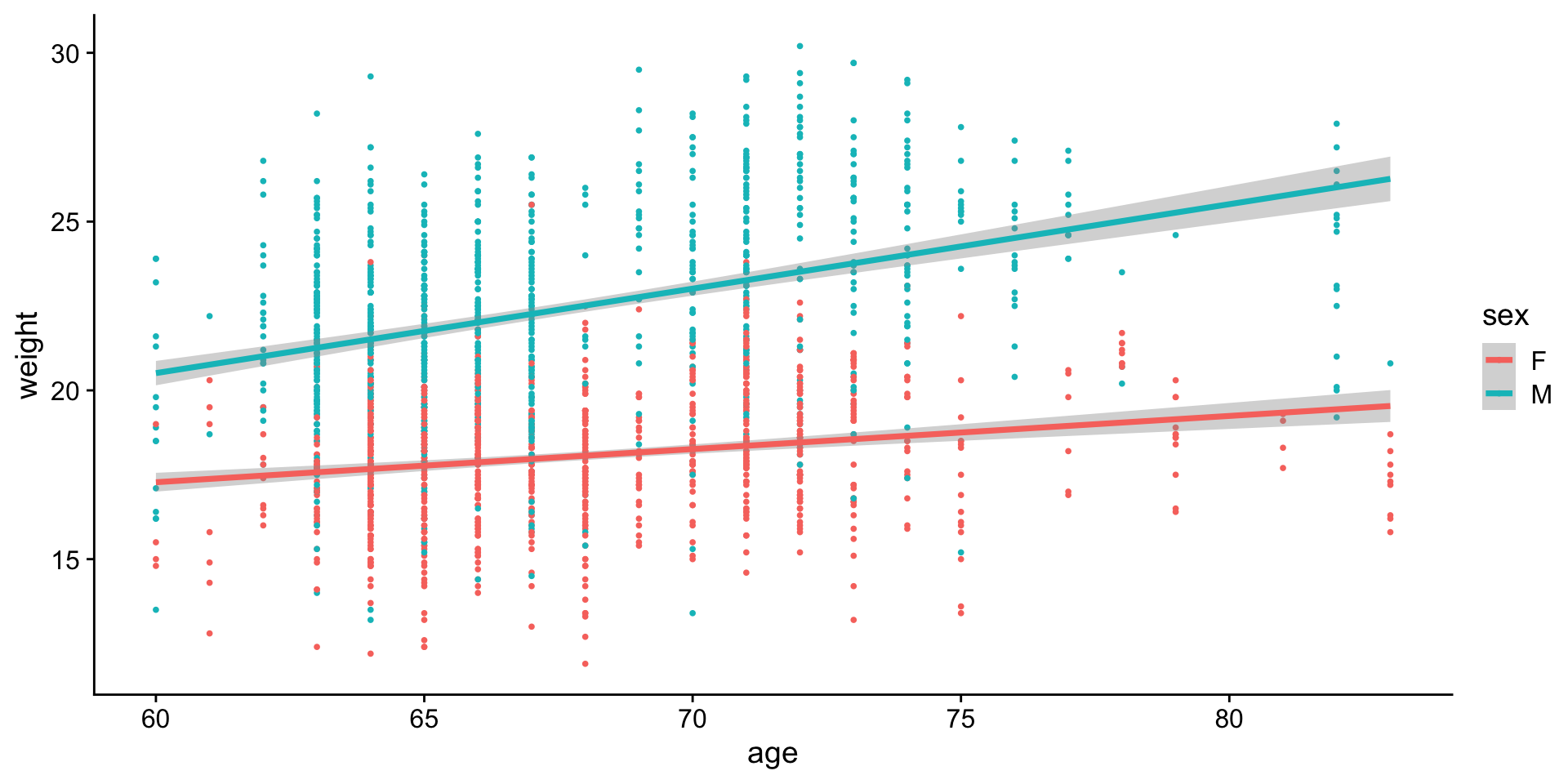
STEP 2: Fit linear model and examine results

fit_wa_sex <- lm(formula = weight ~ 1 + age + sex, data = b)
b_wa_sex <- augment(fit_ws, data = b)

Fit summary:

glance(fit_wa_sex) |>
  gt() |>
  fmt_number(columns = r.squared:statistic, decimals = 3)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.475 0.475 2.418 805.482 8.373684e-250 2 -4100.477 8208.955 8230.897 10401.67 1779 1782

Compare to traditional:

aov(formula = weight ~ 1 + age + sex, data = b) |>
  glance()
# A tibble: 1 x 6
  logLik   AIC   BIC deviance  nobs r.squared
   <dbl> <dbl> <dbl>    <dbl> <int>     <dbl>
1 -4100. 8209. 8231.   10402.  1782     0.475

References

Linear Models Pt.3 - Design Matrices

A Matrix Formulation of the Multiple Regression Model

Doing and reporting your first ANOVA and ANCOVA in R40f2ef

Course website: https://rnabioco.github.io/molb-7950