Stats Bootcamp - class 12

Hypothesis testing

Neelanjan Mukherjee

RNA Bioscience Initiative | CU Anschutz

2024-10-21

Learning objectives

  • Formulate and Execute null hypothesis testing
  • Identify and Perform the proper statistical test for data type/comparison
  • Calculate and Interpret p-values

Hypothesis testing definitions

Hypothesis testing is a statistical analysis that uses sample data to assess two mutually exclusive theories about the properties of a population. Statisticians call these theories the null hypothesis and the alternative hypothesis. A hypothesis test assesses your sample statistic and factors in an estimate of the sample error to determine which hypothesis the data support.

When you can reject the null hypothesis, the results are statistically significant, and your data support the theory that an effect exists at the population level.

Definitions

Effect — the difference between the population value and the null hypothesis value. The effect is also known as population effect or the difference. Typically, you do not know the size of the actual effect. However, you can use a hypothesis test to help you determine whether an effect exists and to estimate its size.

Null Hypothesis or \(\mathcal{H}_0\) — one of two mutually exclusive theories about the properties of the population in hypothesis testing. Typically, the null hypothesis states that there is no effect (i.e., the effect size equals zero).

Alternative Hypothesis or \(\mathcal{H}_1\) — the other theory about the properties of the population in hypothesis testing. Typically, the alternative hypothesis states that a population parameter does not equal the null hypothesis value. In other words, there is a non-zero effect. If your sample contains sufficient evidence, you can reject the null and favor the alternative hypothesis.

Definitions cont.

P-values — the probability of obtaining test results at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct. Lower p-values represent stronger evidence against the null. P-values in conjunction with the significance level determines whether your data favor the null or alternative hypothesis.

Significance Level or \(a\) — an evidentiary standard set before the study. It is the probability that you say there is an effect when there is no effect (the probability of rejecting the null hypothesis given that it is true). Lower significance levels indicate that you require stronger evidence before you will reject the null.It is usually set at or below .05.

Variables definitions

Random variables

Response Variable ( y - aka dependent or outcome variable): this variable is predicted or its variation is explained by the explanatory variable. In an experiment, this is the outcome that is measured following manipulation of the explanatory variable.

Explanatory Variable ( x - aka independent or predictor variable): explains variations in the response variable. In an experiment, it is manipulated by the researcher.

Null hypothesis testing

  1. Examine and specify the variable(s)
  2. Declare null hypothesis \(\mathcal{H}_0\)
  3. Calculate test-statistic, exact p-value

calculating empirical p-value (alternative to 3):
Generate and visualize data reflecting null-distribution
Calculate the frequency of your observation vs all null distribution values

Parametric vs Nonparametric tests

Parametric tests are suitable for normally distributed data.

Nonparametric tests are suitable for any continuous data. Though these tests have their own sets of assumption, you can think of Nonparametric tests as the ranked versions of the corresponding parametric tests.

More on choosing Parametric vs Non-Parametric

Info Parametric Nonparametric
better descriptor mean median
# of samples (N) many few

Appropriate statistical test cheatsheet

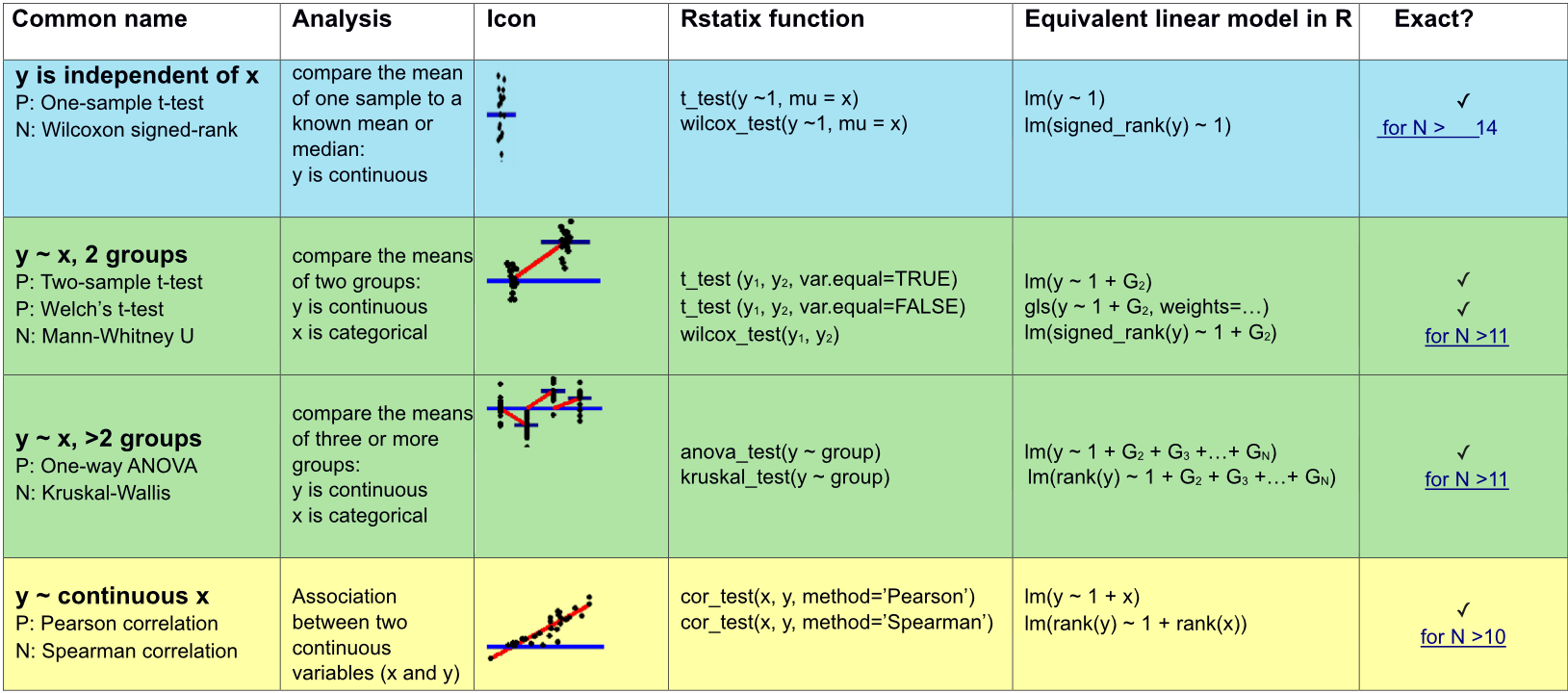
Assumptions of many parametric tests

  1. The data are randomly sampled (independent).
  2. The distribution is approximately normal*.
  3. There is homogeneity of variance (i.e., the variability of the data in each group is similar).

*With many samples (>20) then lack of normality assumption is not a concern due to the central limit theorem. AND shapiro_test() is too sensitive with large number of observations.

Two changes

  1. We are going to use ggpubr rather than ggplot2 - Don’t tell Jay ;)
  • It has great visualization for the stats on the plots.
  • Different syntax!!
    • must use double quotes around “variable names”
  1. Due to reviewer #3, we will pivot to a more “physiologically relevant” data set biochem that consists of mouse measurements.
read_tsv("http://mtweb.cs.ucl.ac.uk/HSMICE/PHENOTYPES/Biochemistry.txt", show_col_types = FALSE) |>
  janitor::clean_names() |>
  colnames()
 [1] "subject_name"            "biochem_albumin"        
 [3] "biochem_alp"             "biochem_alt"            
 [5] "biochem_ast"             "biochem_calcium"        
 [7] "biochem_chloride"        "biochem_creatinine"     
 [9] "biochem_glucose"         "biochem_hdl"            
[11] "biochem_ldl"             "biochem_phosphorous"    
[13] "biochem_potassium"       "biochem_sodium"         
[15] "biochem_tot_cholesterol" "biochem_tot_protein"    
[17] "biochem_triglycerides"   "biochem_urea"           
[19] "end_normal_bw"           "date_study_day"         
[21] "date_season"             "date_month"             
[23] "date_year"               "family"                 
[25] "gender"                  "age"                    
[27] "cage_density"            "litter"

Prepare mouse biochem data

# we are reading the data directly from the internet
biochem <- read_tsv("http://mtweb.cs.ucl.ac.uk/HSMICE/PHENOTYPES/Biochemistry.txt", show_col_types = FALSE) |>
  janitor::clean_names()

# simplify names a bit more
colnames(biochem) <- gsub(pattern = "biochem_", replacement = "", colnames(biochem))

# we are going to simplify this a bit and only keep some columns
keep <- colnames(biochem)[c(1, 6, 9, 14, 15, 24:28)]
biochem <- biochem[, keep]

# get weights for each individual mouse
# careful: did not come with column names
weight <- read_tsv("http://mtweb.cs.ucl.ac.uk/HSMICE/PHENOTYPES/weight", col_names = F, show_col_types = FALSE)

# add column names
colnames(weight) <- c("subject_name", "weight")

# add weight to biochem table and get rid of NAs
# rename gender to sex
b <- inner_join(biochem, weight, by = "subject_name") |>
  na.omit() |>
  rename(sex = gender)

Compare mean of a variable to a known value

\(y\) is independent of \(x\)

\(y\) is continuous

\(x\) is constant

Parametric: One-sample t-test

t_test(y ~ 1, mu = x)

Nonparametric: Wilcoxon signed-rank

wilcox_test(y ~ 1, mu = x)

  1. Examine and specify the variable(s)
  2. Declare null hypothesis \(\mathcal{H}_0\)
  3. Calculate test-statistic, exact p-value

Think did the expression of my gene change…

1. Examine and specify the variable(s)

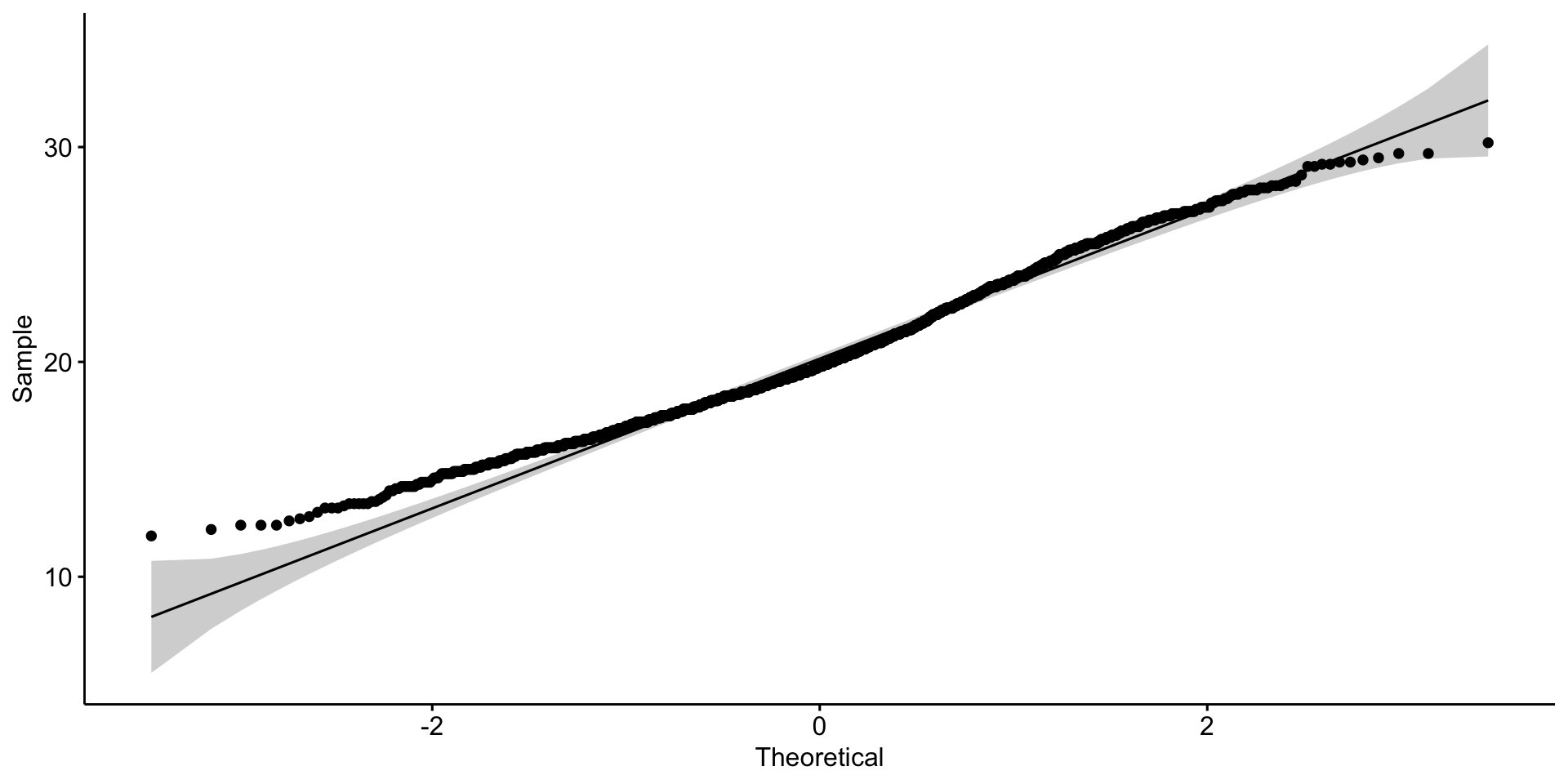
Let’s explore mouse \(weight\)

ggdensity(
  data = b,
  x = "weight",
  add = "mean",
  rug = TRUE
)
Warning: `geom_vline()`: Ignoring `mapping` because `xintercept` was provided.
Warning: `geom_vline()`: Ignoring `data` because `xintercept` was provided.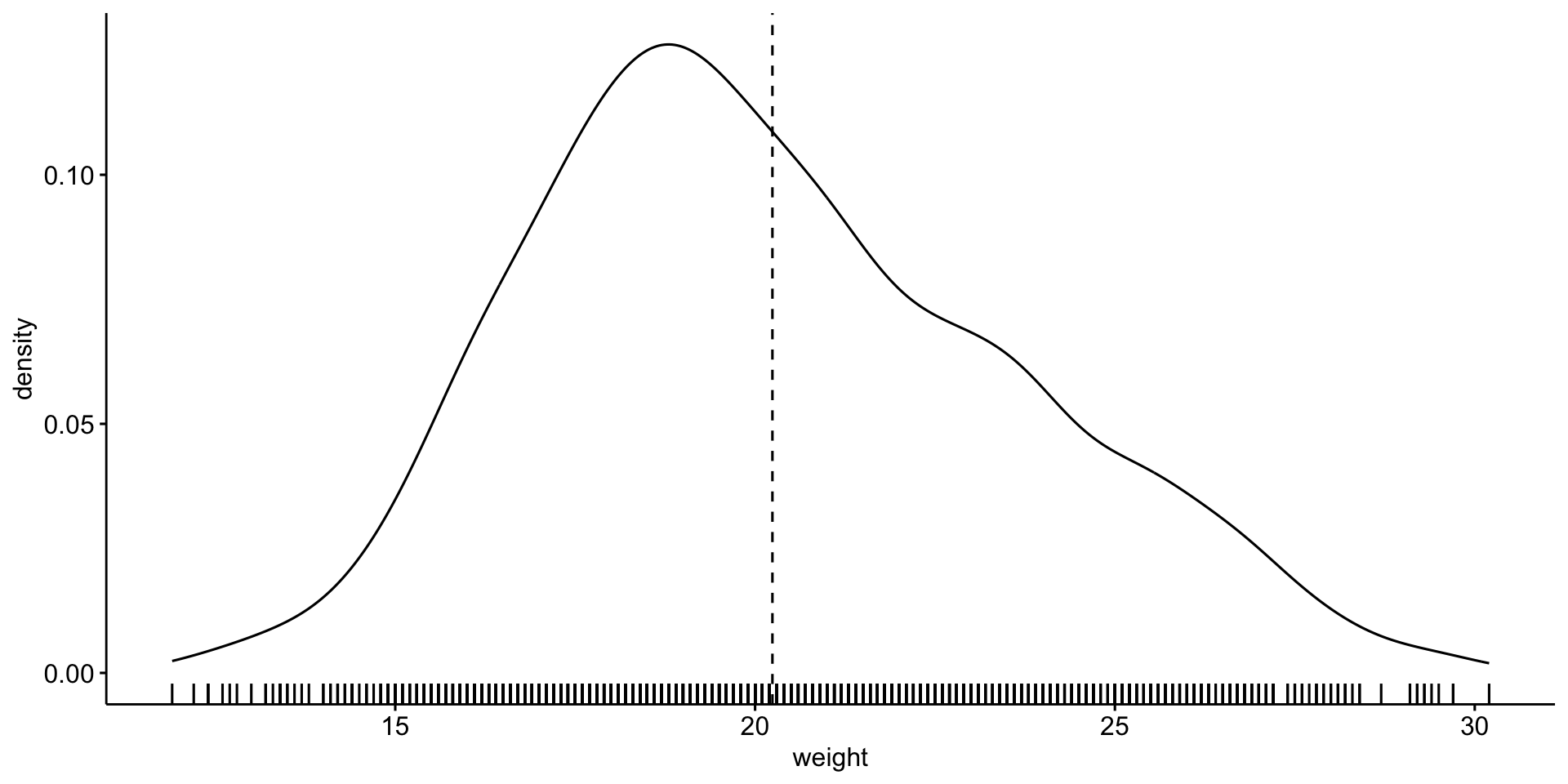

let’s see some summary stats

b |>
  get_summary_stats(
    weight,
    type = "common",
    show = c("mean", "median", "sd")
  )
# A tibble: 1 × 5
  variable     n  mean median    sd
  <fct>    <dbl> <dbl>  <dbl> <dbl>
1 weight    1782  20.2   19.8  3.34

Is it normally distributed?

ggqqplot(
  data = b,
  x = "weight"
)

Looks reasonable

b |>
  shapiro_test(weight)
# A tibble: 1 × 3
  variable statistic        p
  <chr>        <dbl>    <dbl>
1 weight       0.984 3.47e-13

Yikes!

No easy answers…gotta make a call. We’ll try both.

2. Declare null hypothesis \(\mathcal{H}_0\)

Since this is a one-way test, we don’t need to worry if the groups have equal variance (only 1 group). But, we need a standard to compare against. I asked google, how much does a mouse weigh in grams?

Answer: 20-35 g, I’m going with \(27.5 g\) as our standard.

\(\mathcal{H}_0\) is that the mean of mouse \(weight\) can be explained by \(27.5\)

\(weight\) is the response variable

\(27.5\) is the explanatory variable

3. Calculate test-statistic, exact p-value

Nonparametric test:

x <- 27.5 # standard from google

b |>
  wilcox_test(weight ~ 1, mu = x) |>
  gt()
.y. group1 group2 n statistic p
weight 1 null model 1782 2084 1.62e-290

Parametric test:

x <- 27.5 # standard from google

b |>
  t_test(weight ~ 1, mu = x) |>
  gt()
.y. group1 group2 n statistic df p
weight 1 null model 1782 -91.85587 1781 0

P values are well below 0.05

\(\mathcal{H}_0\) is that the mean of mouse \(weight\) can be explained by \(27.5\) is NOT WELL SUPPORTED

So \(27.5 g\) not able to describe weight

Not surprising since our mean mouse weight is 20.2. Don’t believe everything you read on the internet.

Compare mean of two groups

\(y\) is independent of \(x\)

\(y\) is continuous

\(x\) is categorical with 2 groups (factor w/2 levels)

Parametric: Student’s t-test

t_test(y ~ x) more here

need to pay attention to: var.equal paired

Nonparametric: Wilcoxon signed-rank

wilcox_test(y ~ x) more here

need to pay attention to: paired

  1. Examine and specify the variable(s)
  2. Declare null hypothesis \(\mathcal{H}_0\)
  3. Calculate test-statistic, exact p-value

Tangent on Student’s t-test

The T-Distribution, also known as Student’s t-distribution, gets its name from William Sealy Gosset who first published it in English in 1908 in the scientific journal Biometrika using his pseudonym “Student” because his employer preferred staff to use pen names when publishing scientific papers instead of their real name, so he used the name “Student” to hide his identity.

Guinness Brewery in Dublin

1. Examine and specify the variable(s)

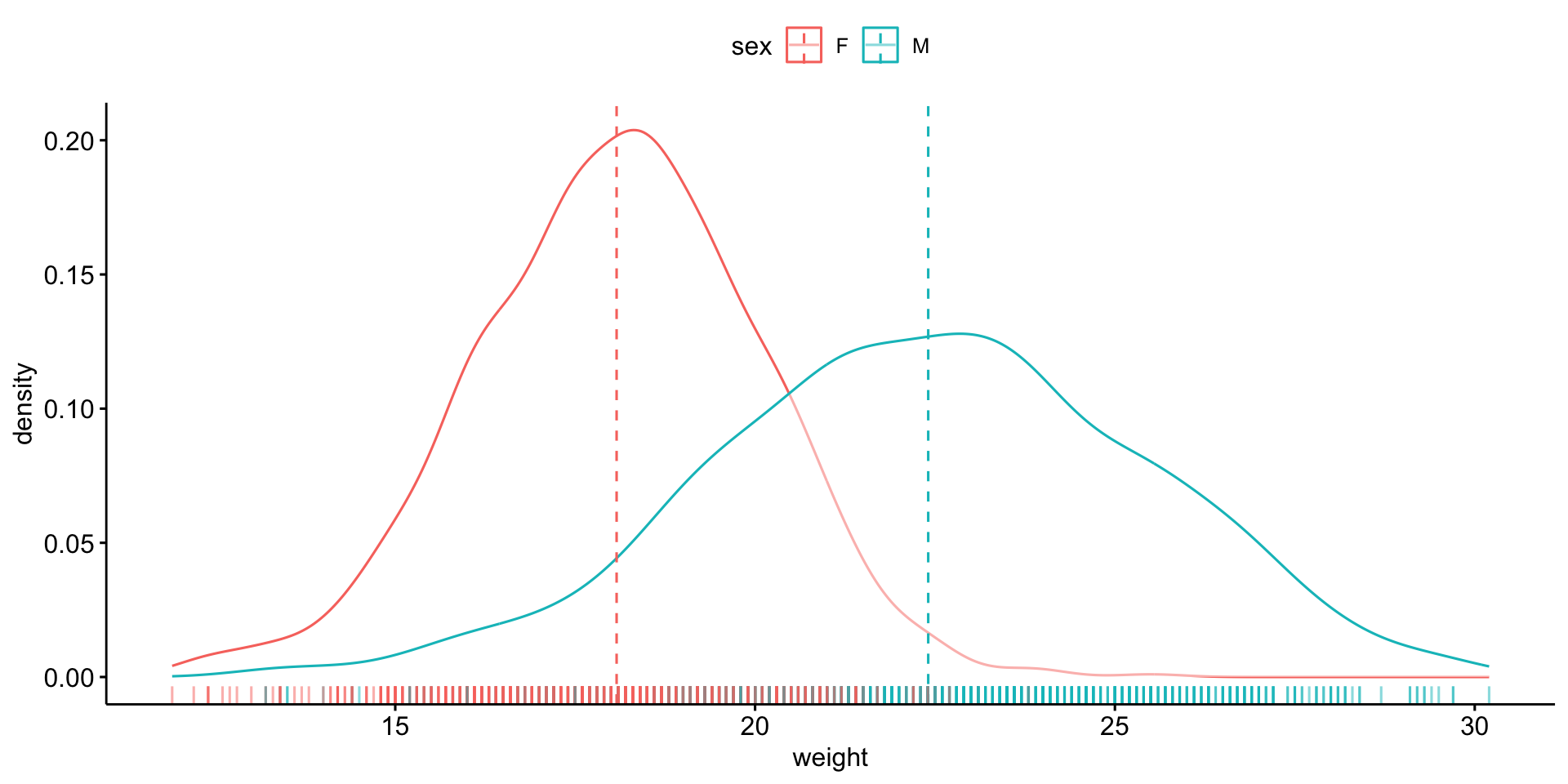
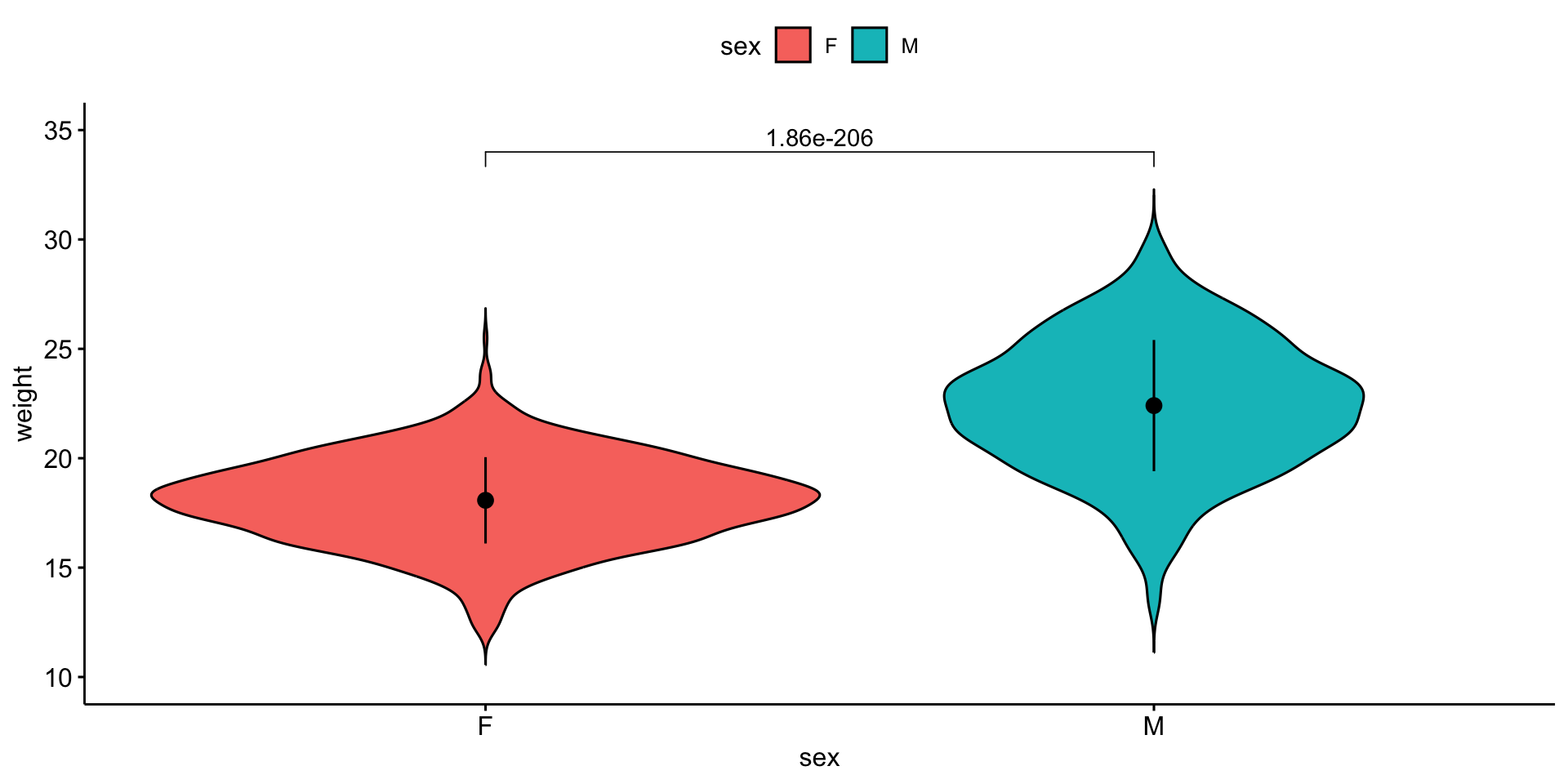
We will compare mouse \(weight\) by \(sex\).

\(weight\) is the response variable

\(sex\) is the explanatory variable

\(y\) ~ \(x\)

\(weight\) ~ \(sex\)

ggdensity(
  data = b,
  color = "sex",
  x = "weight",
  add = "mean",
  rug = TRUE
)

I want the response variable on the \(y\) axis and the explanatory variable on the \(x\) axis.

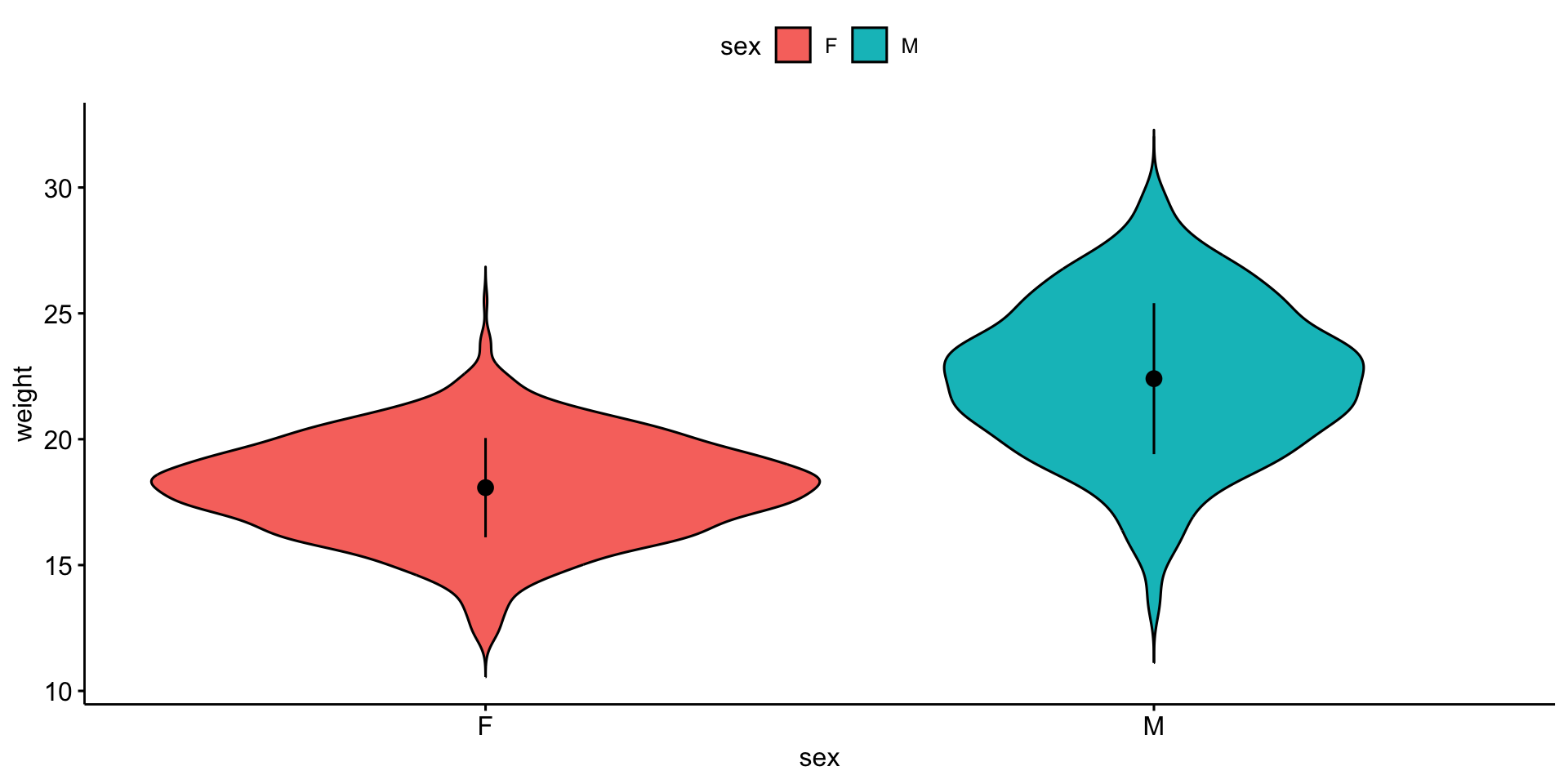
Violin plot

ggviolin(
  data = b,
  y = "weight",
  x = "sex",
  fill = "sex",
  add = "mean_sd"
)

b |>
  group_by(sex) |>
  get_summary_stats(
    weight,
    type = "common",
    show = c("mean", "median", "sd")
  )
# A tibble: 2 × 6
  sex   variable     n  mean median    sd
  <chr> <fct>    <dbl> <dbl>  <dbl> <dbl>
1 F     weight     891  18.1   18.2  1.97
2 M     weight     891  22.4   22.5  3.00

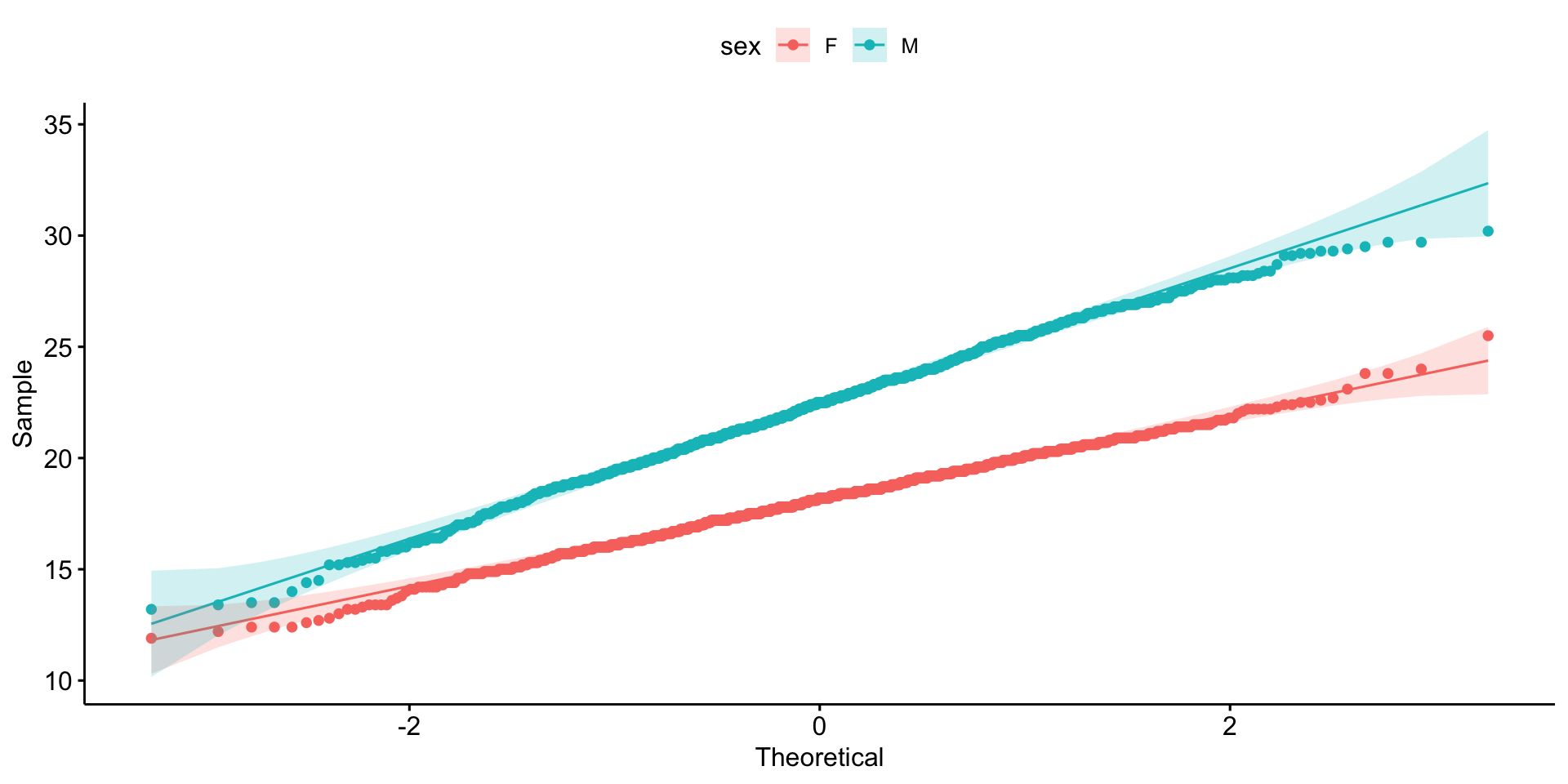
Is it normally distributed?

ggqqplot(
  data = b,
  x = "weight",
  color = "sex"
)

b |>
  group_by(sex) |>
  shapiro_test(weight) |>
  gt()
sex variable statistic p
F weight 0.9973195 0.15030026
M weight 0.9968175 0.07238238

Looks reasonable

Equal variance?

b |>
  levene_test(weight ~ sex) |>
  gt()
Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.
df1 df2 statistic p
1 1780 134.994 3.928697e-30

OK - so we can use t-test, but variance is not equal.

2. Declare null hypothesis \(\mathcal{H}_0\)

\(\mathcal{H}_0\) is that \(sex\) cannot explain \(weight\)

3. Calculate test-statistic, exact p-value

Nonparametric test:

b |>
  wilcox_test(weight ~ sex, ref.group = "F") |>
  gt()
.y. group1 group2 n1 n2 statistic p
weight F M 891 891 90192 1.64e-175

Parametric test:

x <- 27.5 # standard from google

b |>
  t_test(weight ~ sex,
    var.equal = F,
    ref.group = "F"
  ) |>
  gt()
.y. group1 group2 n1 n2 statistic df p
weight F M 891 891 -36.00705 1538.681 1.86e-206

P values are well below 0.05

\(\mathcal{H}_0\) is that \(sex\) cannot explain \(weight\) is NOT WELL SUPPORTED

\(sex\) can explain \(weight\)

Visualize the result

# save statistical test result
statres <- b |>
  t_test(weight ~ sex,
    var.equal = F,
    ref.group = "F"
  )


ggviolin(
  data = b,
  y = "weight",
  x = "sex",
  fill = "sex",
  add = "mean_sd"
) +
  stat_pvalue_manual(
    statres,
    label = "p",
    y.position = 34
  ) +
  ylim(10, 35)

Visualize the result

Compare means of three or more groups

\(y\) is independent of \(x\)

\(y\) is continuous

\(x\) is 2 or more groups of categorical data

Parametric: ANOVA

anova_test(y ~ group) more info

Nonparametric: Kruskal-Wallis test

kruskal_test(y ~ group) more info

  1. Examine and specify the variable(s)
  2. Declare null hypothesis \(\mathcal{H}_0\)
  3. Calculate test-statistic, exact p-value

1. Examine and specify the variable(s)

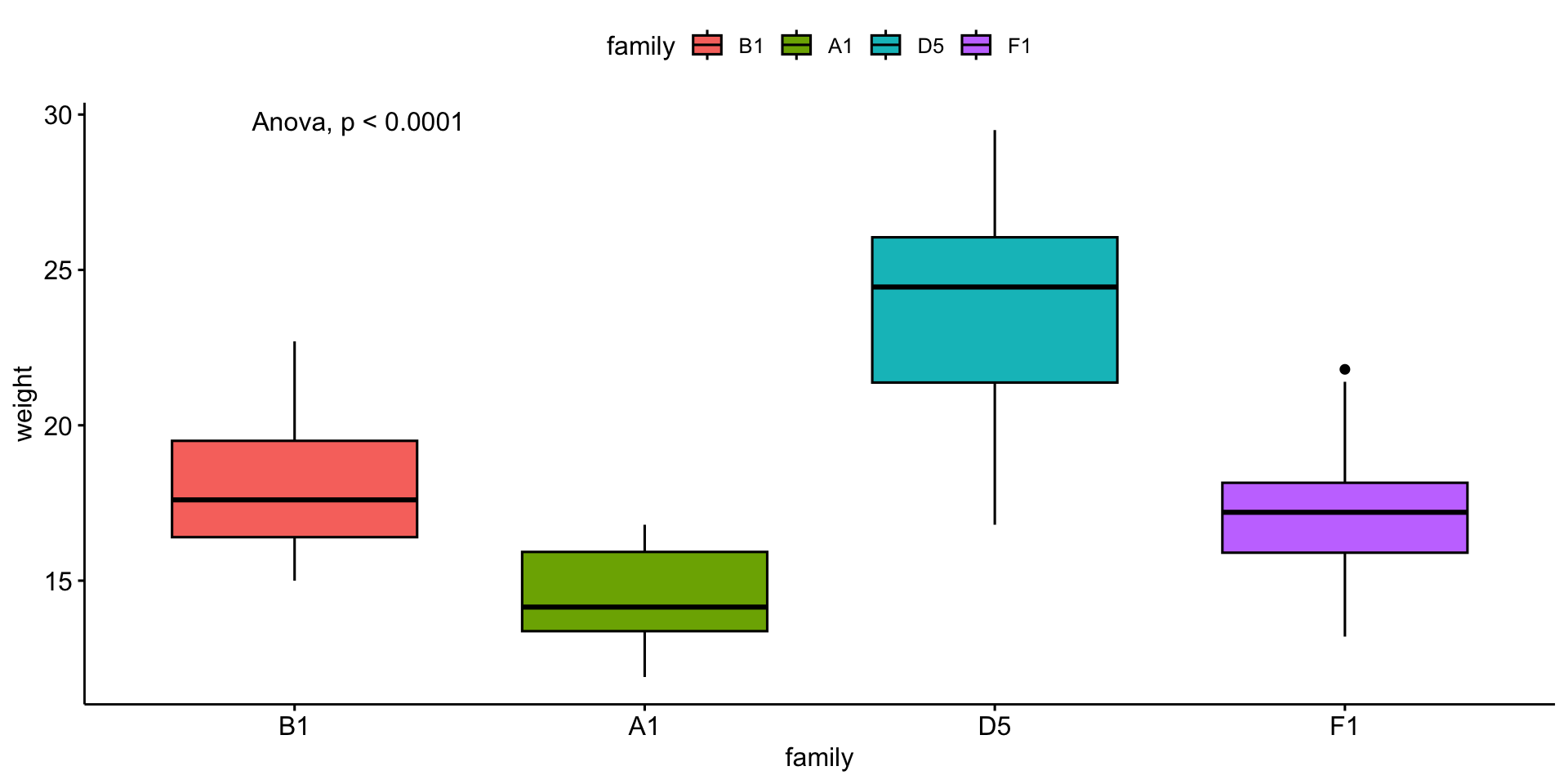
We will compare mouse \(weight\) by \(family\).

\(weight\) is the response variable

\(family\) is the explanatory variable

\(y\) ~ \(x\)

\(weight\) ~ \(family\)

# i have pre-selected some families to compare
myfams <- c(
  "B1.5:E1.4(4) B1.5:A1.4(5)",
  "F1.3:A1.2(3) F1.3:E2.2(3)",
  "A1.3:D1.2(3) A1.3:H1.2(3)",
  "D5.4:G2.3(4) D5.4:C4.3(4)"
)

# only keep the familys in myfams
bfam <- b |>
  filter(family %in% myfams) |>
  droplevels()

# simplify family names and make factor
bfam$family <- gsub(pattern = "\\..*", replacement = "", x = bfam$family) |>
  as.factor()


# make B1 the reference (most similar to overall mean)
bfam$family <- relevel(x = bfam$family, ref = "B1")

Visualize the variable(s)

I want the response variable on the \(y\) axis and the explanatory variable on the \(x\) axis.

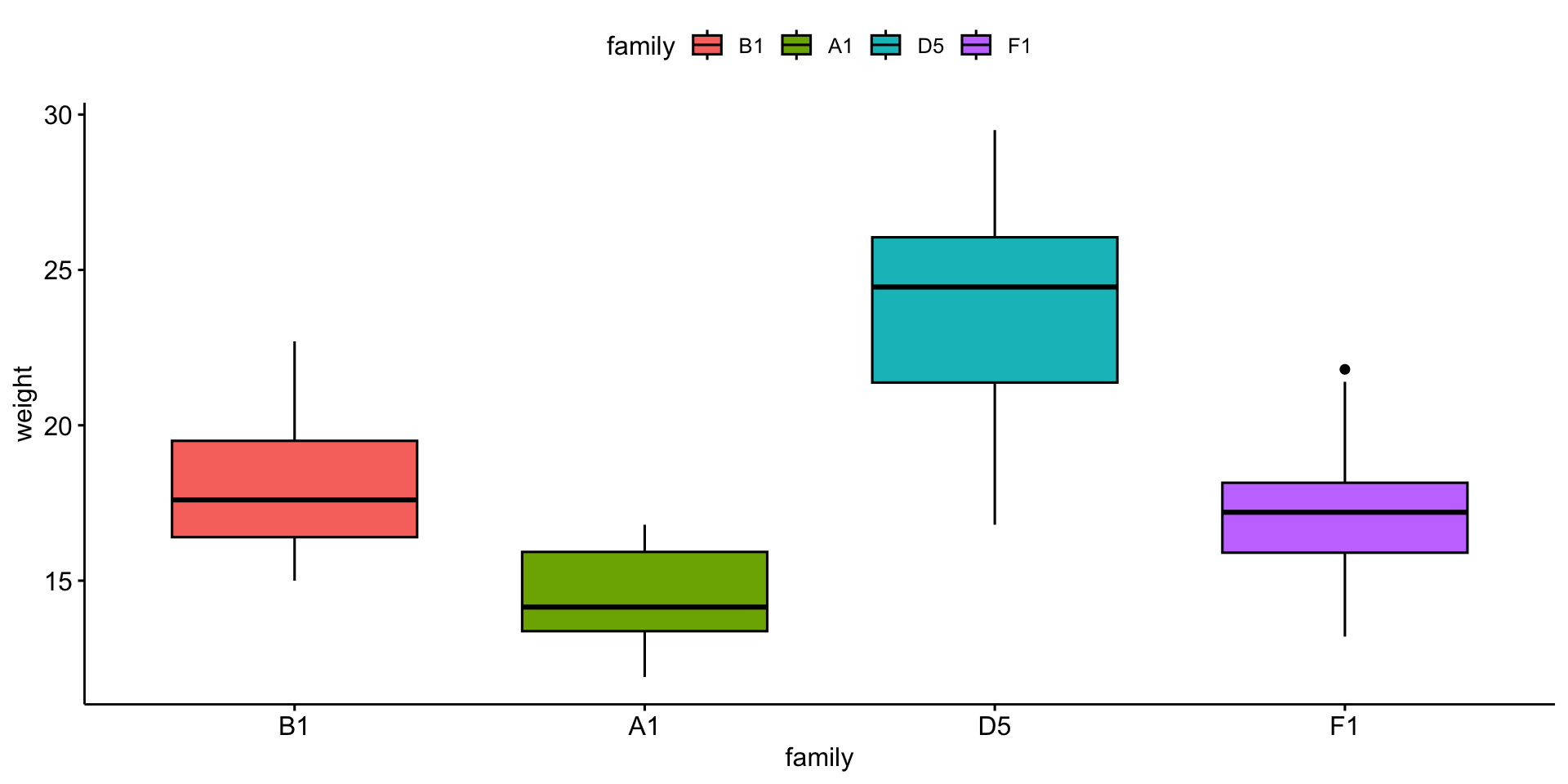
Boxplot

ggboxplot(
  data = bfam,
  y = "weight",
  x = "family",
  fill = "family"
)

bfam |>
  group_by(family) |>
  get_summary_stats(
    weight,
    type = "common",
    show = c("mean", "median", "sd")
  )
# A tibble: 4 × 6
  family variable     n  mean median    sd
  <fct>  <fct>    <dbl> <dbl>  <dbl> <dbl>
1 B1     weight      11  18.1   17.6  2.40
2 A1     weight      12  14.4   14.2  1.57
3 D5     weight      20  23.9   24.4  3.20
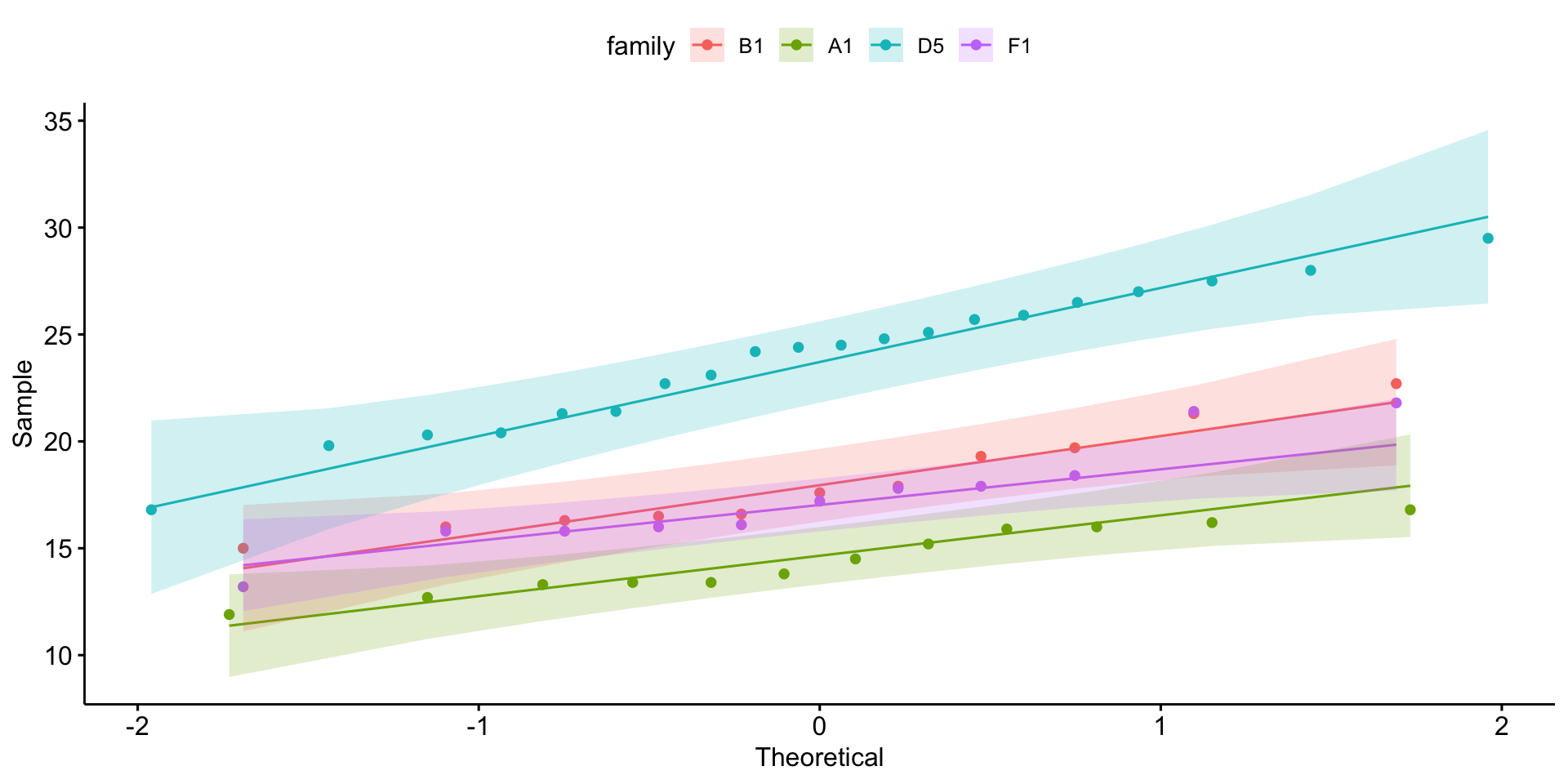
4 F1     weight      11  17.4   17.2  2.51

Is it normally distributed?

ggqqplot(
  data = bfam,
  x = "weight",
  color = "family"
)

bfam |>
  group_by(family) |>
  shapiro_test(weight) |>
  gt()
family variable statistic p
B1 weight 0.9301367 0.4122383
A1 weight 0.9442695 0.5552725
D5 weight 0.9782401 0.9094022
F1 weight 0.9259598 0.3714390

Looks reasonable

Equal variance?

bfam |>
  levene_test(weight ~ family) |>
  gt()
df1 df2 statistic p
3 50 1.38364 0.258576

OK - so we can use anova!

2. Declare null hypothesis \(\mathcal{H}_0\)

\(\mathcal{H}_0\) is that \(family\) cannot explain \(weight\)

3. Calculate test-statistic, exact p-value

Parametric test:

bfam |>
  anova_test(weight ~ family) |>
  gt()
Effect DFn DFd F p p<.05 ges
family 3 50 37.514 7.62e-13 * 0.692

Nonparametric test:

bfam |>
  kruskal_test(weight ~ family) |>
  gt()
.y. n statistic df p method
weight 54 37.07763 3 4.43e-08 Kruskal-Wallis

P values are well below 0.05

\(\mathcal{H}_0\) is that \(family\) cannot explain \(weight\) is NOT WELL SUPPORTED

\(family\) can explain \(weight\)

Visualize the result

# save statistical test result
statres <- bfam |>
  anova_test(weight ~ sex)


ggboxplot(
  data = bfam,
  y = "weight",
  x = "family",
  fill = "family"
) +
  stat_anova_test()

Visualize the result

Multiple pairwise comparisons

Quick aside

# save statistical test result
pairwise <- bfam |>
  t_test(weight ~ family, ref.group = "B1")


ggboxplot(bfam,
  x = "family",
  y = "weight",
  fill = "weight",
) +
  stat_pvalue_manual(
    pairwise,
    label = "p.adj",
    y.position = c(30, 32, 34)
  ) +
  ylim(10, 38)

Notice that not all pairwise differences are significant, yet the ANOVA is significant.

Multiple pairwise comparisons

Warning: The following aesthetics were dropped during statistical transformation: fill
ℹ This can happen when ggplot fails to infer the correct grouping structure in
  the data.
ℹ Did you forget to specify a `group` aesthetic or to convert a numerical
  variable into a factor?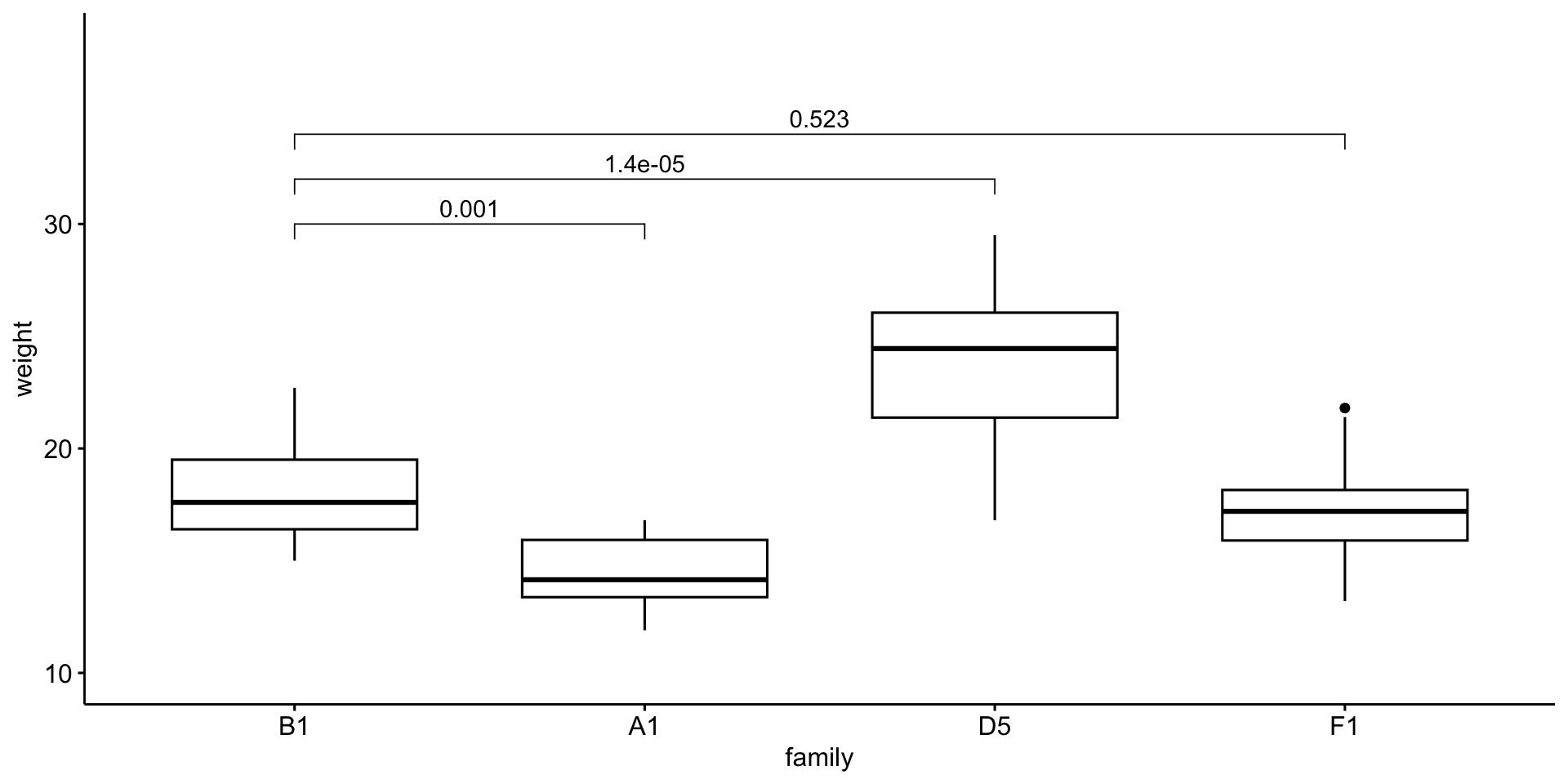

Appropriate statistical test cheatsheet

References

Legal analogy

StatQuest: P Values, clearly explained

StatQuest: How to calculate p-values

The Curious Tale of William Sealy Gosset

Course website: https://rnabioco.github.io/molb-7950